rev/osu? | Buckeye CTF 2022
A 50,000 thread flag checker VM implemented in OpenGL.
Initial Analysis
We’re given an osu-like game written in C++ where you have to click some circles before they expire, and if you click the right ones in the right order, it’ll print out the flag at the end. I’ll be reverse-engineering the linux version for this, as it’s probably the cleanest one in terms of debugging.
The first step is to determine how the beatmap is being loaded. After a bit of poking around, I found that it’s in the LevelSave::LevelSave constructor:
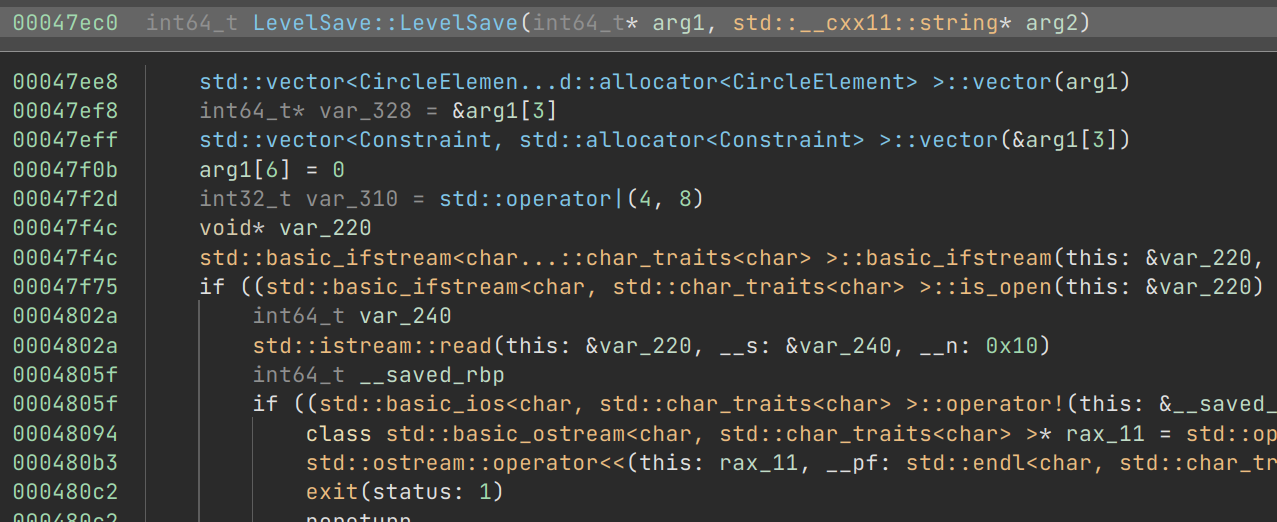
After a bit of reversing, it’s possible to determine the beatmap format:
- An 8-byte little endian number for how many notes there are
- An 8-byte little endian number for how many constraints there are (it’s unclear what these are right now)
- 3 8-byte little endian numbers for each notes
- 4 8-byte little endian numbers followed by 32 bytes of data for each constraint
To figure out what the 3 numbers mean for the notes, we can refer to the symbol name for the CircleElement::CircleElement constructor:
CircleElement::CircleElement(uint64_t, Position, Color, int64_t, char)
Then, looking at the order that parameters are passed in, we can determine that the first number is the position, the second number is the mysterious int64_t, and the third number is the color, and every circle is assigned a unique ID based on its index in the beatmap. It’s possible to do some more reversing to figure out what the second number does, but after printing some values and noticing that it’s incremental, it’s possible to deduce that it’s the tick that the note expires.
Next, we need to figure out where the flag actually is. When the game finishes, that wasn't right :{ is printed at the end. Presumably, if the right circles are clicked, the flag will take its place instead. By searching for references to the “that wasn’t right” string, we can find it referenced at the end of Level::render:

The “that wasn’t right” string is only replaced if every element in the level.offset_0x130 vector is 1. Strangely enough, when searching for references to this vector, the only reference is…binding it as a shader data buffer? So, somehow the shader is populating this vector and we need to figure out how to get it to all be 1.
Here’s the shader that’s being called:
#version 150
in ivec4 r;
in uvec4 code[2];
in int s;
ivec4 r_c;
int s_c;
int t;
out int out_attr;
out vec4 color;
int get1(uint i) {
switch (i) {
case 0u:
return r_c.x;
case 1u:
return r_c.y;
case 2u:
return r_c.z;
case 3u:
return r_c.w;
default:
return 0;
}
}
void set1(uint i, int val) {
switch (i) {
case 0u:
r_c = ivec4(val, r_c.yzw);
break;
case 1u:
r_c = ivec4(r_c.x, val, r_c.zw);
break;
case 2u:
r_c = ivec4(r_c.xy, val, r_c.w);
break;
case 3u:
r_c = ivec4(r_c.xyz, val);
break;
default:
return;
}
}
int get2(uint i) {
return (i == 0u) ? s_c : t;
}
void set2(uint i, int val) {
if (i == 0u) {
s_c = val;
} else {
t = val;
}
}
uint handle_insn(uint insn, uint pc) {
int r1, r2, r3;
uint op = insn & 0x7u;
uint o1 = (insn >> 3) & 0x3u;
uint o2 = (insn >> 5) & 0x3u;
uint o3 = (insn >> 7) & 0x1u;
uint next = pc + 1u;
switch (op) {
case 0u:
case 1u:
case 2u:
case 3u:
r1 = get1(o1);
r2 = get1(o2);
if (op == 0u) {
set2(o3, r1 + r2);
} else if (op == 1u) {
set2(o3, r1 - r2);
} else if (op == 2u) {
set2(o3, r1 & r2);
} else if (op == 3u) {
set2(o3, r1 | r2);
}
break;
case 4u:
r3 = get2(o3);
if (r3 == 0) {
uint off = (o2 << 2) | o1;
next += uint(int(off) - 7);
}
break;
case 5u:
r3 = get2(o3);
if (r3 != 0) {
uint off = (o2 << 2) | o1;
next += uint(int(off) - 7);
}
break;
case 6u:
if (o1 == 0u) {
set1(o2, get2(o3));
} else if (o1 == 1u) {
int z = get1(o2);
set1(o2, get2(o3));
set2(o3, z);
} else if (o1 == 2u) {
set1(o2, int(o3));
} else if (o1 == 3u) {
set1(o2, 0xffffffff);
}
break;
case 7u:
r1 = get1(o1);
r2 = get1(o2);
if (o1 == o2) {
set2(o3, (r1 < 0) ? 1 : 0);
} else {
set2(o3, (r1 < r2) ? 1 : 0);
}
break;
}
return next;
}
uint fetch_insn_4(uint v, uint idx) {
switch (idx) {
case 0u:
return v & 0xffu;
case 1u:
return (v >> 8) & 0xffu;
case 2u:
return (v >> 16) & 0xffu;
case 3u:
return (v >> 24) & 0xffu;
}
}
uint fetch_insn_16(uvec4 v, uint idx) {
switch (idx >> 2) {
case 0u:
return fetch_insn_4(v.x, idx & 0x3u);
case 1u:
return fetch_insn_4(v.y, idx & 0x3u);
case 2u:
return fetch_insn_4(v.z, idx & 0x3u);
case 3u:
return fetch_insn_4(v.w, idx & 0x3u);
}
}
uint fetch_insn(uint pc) {
if ((pc >> 4) == 0u) {
return fetch_insn_16(code[0], pc & 0xfu);
} else {
return fetch_insn_16(code[1], pc & 0xfu);
}
}
void main()
{
r_c = r;
s_c = s;
uint count = 0u;
uint pc = 0u;
while (count < 10000u && pc < 32u) {
uint insn = fetch_insn(pc);
pc = handle_insn(insn, pc);
count += 1u;
}
out_attr = s_c;
color = vec4(0.0, 0.0, 1.0, 1.0);
gl_Position = vec4(0, 0, 0, 0);
}
This is a VM interpreter! 32 bytes of bytecode are inputted through code, and each instruction is 1 byte. The bottom 3 bits are the opcode, the next 2 bits are an operand, the next 2 are another, and the next 1 is another. There are 6 registers, which I’ll refer to as s, t, and r# where # is a number from 0 to 3, inclusive. After skimming the interpreter, opcodes 0-3 are addition, subtraction, bitwise and, and bitwise or, respectively. Opcodes 4 and 5 are conditional jumps, opcode 6 has various ways to move around registers, and opcode 7 has integer comparisons. We’ll be going more in depth when we’re actually writing the disassembler for the bytecode; for now we just want to figure out how this is being called.
The only reference to the relevant shader is in the Level::checker function:

If I’m being honest, I had no clue what this function did when solving the challenge and I’m still not quite sure how it works. However, what’s important is that it’s binding the previous values of level.offset_0x130 to a vertex attribute array, a vector containing the last 32 bytes of each constraint to another, and a mysterious vector to another. It then invokes the shader on these vertices, essentially running the VM on all of these vertices simultaneously in the GPU.
Searching for references to that mysterious vector, we can find one in Level::handle_click:

So, there’s some map<uint64_t, vector<uint64_t>>, that maps the note ID to indices in this mysterious vector, and then assigns the “score time” (the tick the note was clicked, or -1 if it wasn’t) to all the indices. Searching for references to this map, we find it in Level::build_index:

This uses the first 4 8-byte numbers in each constraint and essentially creates a reverse mapping, mapping each value to the indices in which they occur. Combining this with the previous information along with some debugging (my teammate used renderdoc to dump the inputs for every frame), we can determine what the input data is:
s: The previous value of s
t: uninitialized
r0-r3: The score times of the notes at the indices given by the first 4 numbers of the constraint
code: The last 32 bytes of the constraint
All we have to do is figure out how to satisfy these constraints.
Analyzing the Bytecode
Now that we know what we’re working with, we can start parsing the notes and constraints.
def u64(x):
return int.from_bytes(x, "little")
with open("game.beatmap", "rb") as f:
data = f.read()
nnotes = u64(data[0:8]) # first 8 bytes is number of notes
ncons = u64(data[8:16]) # next 8 is number of constraints
notes = []
o = 16
# notes are 24 bytes each, represent them as 3 8-byte ints
for i in range(nnotes):
x = data[o:o + 24]
notes.append([u64(x[i:i + 8]) for i in range(0, len(x), 8)])
o += 24
cons = []
# constraints are 64 bytes each, represent them as 4 8-byte ints and a 32-byte bytestring
for i in range(ncons):
x = data[o:o + 64]
cons.append(([u64(x[i:i + 8]) for i in range(0, 32, 8)], x[32:]))
And we can verify that they do look correct:
>>> [hex(x) for x in notes[0]]
['0x3dcccccdbf000000', '0x118', '0xff']
>>> cons[0]
([1556, 657, 1238, 1028], b'\x87\x86\xaf\xa6\xd7\xc6\xa0\xe6\xd8\x86\xf6\xf8\xe6\xe7\xf6\xc4~n\x80\x80\x80\x80\x80\x80\x80\x80\x80\x80\x80\x80\x80\x80')
Now, we can basically rewrite the bytecode interpreter in python in order to disassemble it:
# format the s/t registers
def reg(x):
return ["s", "t"][x]
# disassemble a single byte
def disas_one(b, i):
opcode = b & 0x7
o1 = (b >> 3) & 0x3
o2 = (b >> 5) & 0x3
o3 = (b >> 7) & 0x1
if opcode == 0:
return f"{reg(o3)} = r{o1} + r{o2}"
elif opcode == 1:
return f"{reg(o3)} = r{o1} - r{o2}"
elif opcode == 2:
return f"{reg(o3)} = r{o1} & r{o2}"
elif opcode == 3:
return f"{reg(o3)} = r{o1} | r{o2}"
elif opcode == 4:
off = (o2 << 2) | o1
off -= 7
target = i + 1 + off
return f"if !{reg(o3)} goto {target:02x}"
elif opcode == 5:
off = (o2 << 2) | o1
off -= 7
target = i + 1 + off
return f"if {reg(o3)} goto {target:02x}"
elif opcode == 6:
if o1 == 0:
return f"r{o2} = {reg(o3)}"
elif o1 == 1:
return f"swap(r{o2}, {reg(o3)})"
elif o1 == 2:
return f"r{o2} = {o3}"
elif o1 == 3:
return f"r{o2} = -1"
elif opcode == 7:
if o1 == o2:
return f"{reg(o3)} = r{o1} < 0"
else:
return f"{reg(o3)} = r{o1} < r{o2}"
# diassemble the full bytecode
def disas(b):
dis = []
for i in range(len(b)):
dis.append(f"{i:02x}: {disas_one(b[i], i) or '???'}")
return "\n".join(dis)
Now that we have a working disassembler, it’s time to actually look at the bytecode. Here’s the disassembly for the first constraint:
00: t = r0 < 0
01: r0 = t
02: t = r1 < 0
03: r1 = t
04: t = r2 < 0
05: r2 = t
06: t = r0 + r1
07: r3 = t
08: t = r3 + r2
09: r0 = t
0a: r3 = 1
0b: t = r3 + r3
0c: r3 = t
0d: t = r0 < r3
0e: r3 = 1
0f: if !t goto 11
10: r3 = -1
11: swap(r3, s)
12: t = r0 + r0
13: t = r0 + r0
14: t = r0 + r0
15: t = r0 + r0
16: t = r0 + r0
17: t = r0 + r0
18: t = r0 + r0
19: t = r0 + r0
1a: t = r0 + r0
1b: t = r0 + r0
1c: t = r0 + r0
1d: t = r0 + r0
1e: t = r0 + r0
1f: t = r0 + r0
This is essentially checking that out of the first 3 notes (the fourth is discarded), at least 2 have been missed. Note that the tick in which you click the note doesn’t matter; all that matters is if it’s -1 or not. If you check the other constraints, you’ll notice that most of them, except 2 special cases, are like this.
Here’s one of the special cases (with the t = r0 + r0 trimmed off the end):
00: r3 = 1
01: t = r0 < 0
02: if t goto 09
03: t = r1 < 0
04: if t goto 09
05: t = r2 < 0
06: if t goto 09
07: t = r0 - r0
08: if !t goto 0a
09: r3 = -1
0a: t = r0 < r1
0b: if !t goto 10
0c: t = r1 < r2
0d: if !t goto 10
0e: t = r0 - r0
0f: if !t goto 11
10: r3 = -1
11: swap(r3, s)
This essentially checks that the first 3 notes are sequentially clicked. The other special case is similar, except that it doesn’t require that the notes are clicked:
00: swap(r3, s)
01: t = r3 < 0
02: if t goto 08
03: r3 = 1
04: t = r1 < 0
05: if t goto 09
06: t = r0 < 0
07: if !t goto 09
08: r3 = -1
09: t = r2 < 0
0a: if t goto 0e
0b: t = r1 < 0
0c: if !t goto 0e
0d: r3 = -1
0e: swap(r3, s)
Getting the Flag
So, we have a list of notes which have to be clicked within 30 ticks of their expiration, along with a list of constraints on if and when they should be clicked. Considering there are 50,000 of these, it’s pretty impractical to reverse them by hand. So, we’ll be using z3 to solve for the tick times. We can handle the two special cases, and for the rest, we can brute force all 16 possibilities (4 notes and each one is either -1 or not), see which ones work, and add them to the solver. This will also require us to write our own version of the VM interpreter, but luckily it’s not very different from the disassembler.
def simulate(bc, r):
s = [1, 0]
r = list(r)
ip = 0
while ip < len(bc):
nextip = ip + 1
b = bc[ip]
opcode = b & 0x7
o1 = (b >> 3) & 0x3
o2 = (b >> 5) & 0x3
o3 = (b >> 7) & 0x1
if opcode == 0:
s[o3] = r[o1] + r[o2]
elif opcode == 1:
s[o3] = r[o1] - r[o2]
elif opcode == 2:
s[o3] = r[o1] & r[o2]
elif opcode == 3:
s[o3] = r[o1] | r[o2]
elif opcode == 4:
if s[o3] == 0:
off = (o2 << 2) | o1
off -= 7
nextip += off
elif opcode == 5:
if s[o3] != 0:
off = (o2 << 2) | o1
off -= 7
nextip += off
elif opcode == 6:
if o1 == 0:
r[o2] = s[o3]
elif o1 == 1:
(r[o2], s[o3]) = (s[o3], r[o2])
elif o1 == 2:
r[o2] = o3
elif o1 == 3:
r[o2] = -1
elif opcode == 7:
if o1 == o2:
s[o3] = 1 if r[o1] < 0 else 0
else:
s[o3] = 1 if r[o1] < r[o2] else 0
ip = nextip
return s[0]
s = Solver()
nsyms = [Int(f"n_{i}") for i in range(len(notes))]
for i in range(len(nsyms)):
# notes are either -1 or within 30 ticks of the expiration
s.add(Or(nsyms[i] == -1, And(nsyms[i] >= notes[i][1] - 0x1d, nsyms[i] <= notes[i][1])))
for [rs, bc] in tqdm(cons):
d = disas(bc)
# special case 1
if "r0 < r1" in d:
s.add(nsyms[rs[0]] != -1)
s.add(nsyms[rs[1]] != -1)
s.add(nsyms[rs[2]] != -1)
s.add(nsyms[rs[0]] < nsyms[rs[1]])
s.add(nsyms[rs[1]] < nsyms[rs[2]])
# special case 2
elif "00: swap(r3, s)" in d:
s.add(Or(nsyms[rs[1]] == -1, And(nsyms[rs[0]] != -1, nsyms[rs[0]] < nsyms[rs[1]])))
s.add(Or(nsyms[rs[2]] == -1, And(nsyms[rs[1]] != -1, nsyms[rs[1]] < nsyms[rs[2]])))
else:
sice = []
# brute force all 16 cases
for x in itertools.product((-1, 1), repeat=4):
res = simulate(bc, x)
if res == 1:
deet = []
# add the proper constraints
for i in range(4):
if x[i] == -1:
deet.append(nsyms[rs[i]] == -1)
else:
deet.append(nsyms[rs[i]] != -1)
sice.append(And(*deet))
s.add(Or(*sice))
Now, we have a model with the ticks that every note should be clicked! There’s still an issue where 2 notes can be clicked at the same time, so we just need to add the constraint that all the notes that are clicked are distinct, then we can recreate the flag printing routine and get the flag:
print(s.check())
m = s.model()
s.add(Distinct(*(n for n in nsyms if m[n].as_long() > -1)))
print(s.check())
m = s.model()
stuff = [(i, m[n].as_long()) for (i, n) in enumerate(nsyms)]
stuff = [x for x in stuff if x[1] != -1]
stuff.sort(key=lambda x: x[1])
binary = "".join(str(x[0] & 1) for x in stuff)
flag = bytes(int(binary[i:i + 8][::-1], 2) for i in range(0, len(binary), 8))
print(flag)
buckeye{d0nt_t41k_t0_m3_0r_my_50000_thr34d_vm_3v3r_4g41n_btw_d1d_y0u_us3_SAT_0r_SMT}
Appendix
Here’s the solve script in full:
from z3 import *
import itertools
from tqdm import tqdm
def u64(x):
return int.from_bytes(x, "little")
with open("game.beatmap", "rb") as f:
data = f.read()
nnotes = u64(data[0:8])
ncons = u64(data[8:16])
notes = []
o = 16
for i in range(nnotes):
x = data[o:o + 24]
notes.append([u64(x[i:i + 8]) for i in range(0, len(x), 8)])
o += 24
cons = []
for i in range(ncons):
x = data[o:o + 64]
cons.append(([u64(x[i:i + 8]) for i in range(0, 32, 8)], x[32:]))
o += 64
# format the s/t registers
def reg(x):
return ["s", "t"][x]
# disassemble a single byte
def disas_one(b, i):
opcode = b & 0x7
o1 = (b >> 3) & 0x3
o2 = (b >> 5) & 0x3
o3 = (b >> 7) & 0x1
if opcode == 0:
return f"{reg(o3)} = r{o1} + r{o2}"
elif opcode == 1:
return f"{reg(o3)} = r{o1} - r{o2}"
elif opcode == 2:
return f"{reg(o3)} = r{o1} & r{o2}"
elif opcode == 3:
return f"{reg(o3)} = r{o1} | r{o2}"
elif opcode == 4:
off = (o2 << 2) | o1
off -= 7
target = i + 1 + off
return f"if !{reg(o3)} goto {target:02x}"
elif opcode == 5:
off = (o2 << 2) | o1
off -= 7
target = i + 1 + off
return f"if {reg(o3)} goto {target:02x}"
elif opcode == 6:
if o1 == 0:
return f"r{o2} = {reg(o3)}"
elif o1 == 1:
return f"swap(r{o2}, {reg(o3)})"
elif o1 == 2:
return f"r{o2} = {o3}"
elif o1 == 3:
return f"r{o2} = -1"
elif opcode == 7:
if o1 == o2:
return f"{reg(o3)} = r{o1} < 0"
else:
return f"{reg(o3)} = r{o1} < r{o2}"
# diassemble the full bytecode
def disas(b):
dis = []
for i in range(len(b)):
dis.append(f"{i:02x}: {disas_one(b[i], i) or '???'}")
return "\n".join(dis)
def simulate(bc, r):
s = [1, 0]
r = list(r)
ip = 0
while ip < len(bc):
nextip = ip + 1
b = bc[ip]
opcode = b & 0x7
o1 = (b >> 3) & 0x3
o2 = (b >> 5) & 0x3
o3 = (b >> 7) & 0x1
if opcode == 0:
s[o3] = r[o1] + r[o2]
elif opcode == 1:
s[o3] = r[o1] - r[o2]
elif opcode == 2:
s[o3] = r[o1] & r[o2]
elif opcode == 3:
s[o3] = r[o1] | r[o2]
elif opcode == 4:
if s[o3] == 0:
off = (o2 << 2) | o1
off -= 7
nextip += off
elif opcode == 5:
if s[o3] != 0:
off = (o2 << 2) | o1
off -= 7
nextip += off
elif opcode == 6:
if o1 == 0:
r[o2] = s[o3]
elif o1 == 1:
(r[o2], s[o3]) = (s[o3], r[o2])
elif o1 == 2:
r[o2] = o3
elif o1 == 3:
r[o2] = -1
elif opcode == 7:
if o1 == o2:
s[o3] = 1 if r[o1] < 0 else 0
else:
s[o3] = 1 if r[o1] < r[o2] else 0
ip = nextip
return s[0]
s = Solver()
nsyms = [Int(f"n_{i}") for i in range(len(notes))]
for i in range(len(nsyms)):
s.add(Or(nsyms[i] == -1, And(nsyms[i] >= notes[i][1] - 0x1d, nsyms[i] <= notes[i][1])))
for [rs, bc] in tqdm(cons):
d = disas(bc)
if "r0 < r1" in d:
s.add(nsyms[rs[0]] != -1)
s.add(nsyms[rs[1]] != -1)
s.add(nsyms[rs[2]] != -1)
s.add(nsyms[rs[0]] < nsyms[rs[1]])
s.add(nsyms[rs[1]] < nsyms[rs[2]])
elif "00: swap(r3, s)" in d:
s.add(Or(nsyms[rs[1]] == -1, And(nsyms[rs[0]] != -1, nsyms[rs[0]] < nsyms[rs[1]])))
s.add(Or(nsyms[rs[2]] == -1, And(nsyms[rs[1]] != -1, nsyms[rs[1]] < nsyms[rs[2]])))
else:
sice = []
for x in itertools.product((-1, 1), repeat=4):
res = simulate(bc, x)
if res == 1:
deet = []
for i in range(4):
if x[i] == -1:
deet.append(nsyms[rs[i]] == -1)
else:
deet.append(nsyms[rs[i]] != -1)
sice.append(And(*deet))
s.add(Or(*sice))
print(s.check())
m = s.model()
s.add(Distinct(*(n for n in nsyms if m[n].as_long() > -1)))
print(s.check())
m = s.model()
stuff = [(i, m[n].as_long()) for (i, n) in enumerate(nsyms)]
stuff = [x for x in stuff if x[1] != -1]
stuff.sort(key=lambda x: x[1])
binary = "".join(str(x[0] & 1) for x in stuff)
flag = bytes(int(binary[i:i + 8][::-1], 2) for i in range(0, len(binary), 8))
print(flag)